Tolerance-caculator

이론 정리

1. 누적 공차

• 가공 부품들을 조립했을 때 누적되어 발생하는 공차를 누적 공차 또는 조립 공차라고 함.
  
  

2. 공차 분석의 종류

• Worst Case: 각 공차의 단순 합
• Root Sum Square: 정규분포에 따른 통계적 합산
• 회사 자체 기준: Wors Case와 RSS의 조합
  
  

3. 누적 공차 수식

• Worst Case:
  • $n$은 부품 수, $T_{i}$은 각각의 공차일 때 모두 더함.

\[T_{sum} = \displaystyle \sum_{i = 1}^{n} T_i\]

• RSS:
  • 각각의 공차의 제곱의 합의 제곱근을 구하여 누적 공차를 구함.

\[T_{sum} = \sqrt{ \displaystyle \sum_{i = 1}^{n} T_i^2 }\]

• 혼합 방법:
  • 근무했던 직장의 자체 규격으로, 부품 수가 2개인 경우 Worst Case와 동일하고 부품 수가 많을 수록 RSS에 가까워짐

\[T_{sum} = \frac{(n-2) \sqrt{ \displaystyle \sum_{i=1}^{n} T_i^2 } + 2\displaystyle \sum_{i=1}^{n} T_i}{n}\]

4. 예시 적용

• 다음과 같이 공차를 가진 9개 치수가 있는 조립품이 있을 때 $d0$의 누적 공차 구하기

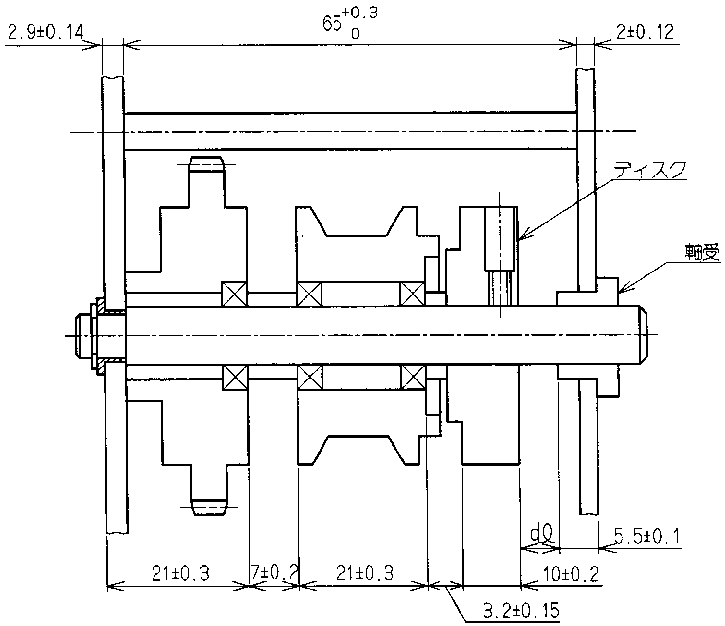</img>

• 편측 공차 치수는 양측 공차로 환산하여 계산

\[65_{0}^{+0.3} \to 65.15\pm0.15\]

• 치수 계산은 치수 누적 방향에 유의하여 계산

\[m = -10-3.2-21-7-21+2.9+65.15+2-5.5 = 2.35\]

• 각 방식별로 공차 계산

\(T_{Worst Case} = 0.2 + 0.15 + 0.3 + 0.2 + 0.3 + 0.14 + 0.15 + 0.12 + 0.1 = 1.66\) \(\therefore 2.35 \pm 1.66\)

\(T_{RSS} = \sqrt{0.2^2 + 0.15^2 + 0.3^2 + 0.2^2 + 0.3^2 + 0.14^2 + 0.15^2 + 0.12^2 + 0.1^2} = 0.59\) \(\therefore 2.35 \pm 0.59\)

\(T_{Combination} = \frac{(9-2)\sqrt{0.2^2 +... + 0.1^2}+2(0.2+ ... + 0.1)}{9} = 0.83\) \(\therefore 2.35 \pm 0.83\)

---